Tengo el gusto de invitarlos al seminario de álgebra y teoría de números de esta semana.
Los esperamos.
Título: Algunas observaciones al polinomio 
Expositor: Víctor Ramírez
Martes, 2 de febrero
Lugar: Sala Mischa Cotlar, MYS 128.
Hora: 12:30 pm.
Resumen:
 |
| Klauber triangle with prime numbers generated by Euler's polynomial x2 − x + 41 highlighted. |
En 1772, Euler obseva que el polinomio 
toma valores primos al sustituir x por 0, 1, 2, ......,39.
En
1936, Lehmer [2] observa que: si 
y toma valores primos
al sustituir x por 0, 1, 2, ......,
; entonces 
es un dominio de
factorización única. Aquí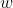 
denota una raíz compleja de y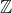 
el
conjunto de los números enteros.
En 1974, Szekeres
[3] demuestra el reciproco del criterio de Lehmer, y hace notar que su
resultado no aparece explicitamente en la literarura.
En 1912, Rabinowitsh [1] establece el siguiente resultado:
Teorema. Sea 
un número primo. Las condiciones siguientes son equivalentes:
(1) toma valores primos al sustituir x por 0, 1, 2, ......,
(2) El cuerpo cuadrático complejo 
tiene número de clase igual a 1
Aquí 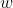denota una raíz compleja de y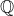 
el conjunto de los números racionales
El
mismo año, Frobenius demuestra que (2) implica (1). En 1981, Ayoub
& Chowla [4] demuestran nuevamete que (2) implica (1). Para más
detalles de discusión de estos resultados véase [5, 6].
Todos
estos resultados requieren de largas digreciones para su demostración.
El propósito de este trabajo es brindar una demostración sencilla del
criterio de Lehmer y de su reciproco.
Referencias
1.. G. Rabinovitch. Eindeutigkeit der Zerlegung in Primzahlfaktoren in quadratischen Zahlk¨orper. 418–421
2.. D. H. Lehmer. On the function x2 + x + A. Sphinx, 6: 212–214
3. G. Szekeres. On the number of divisors of x2+x+A. J. Nb.Th., 6:434–442
4.. R. G. Ayoub and S. Chowla. On Euler’s polynomial. J. Nb. Th., 13:443–445
5. P. Ribenboim. The New Book of Prime Number Records. Springer-Verlag, New York.
6. H. Cohn. Advanced Number Theory. Dover, New York.
No hay comentarios.:
Publicar un comentario